DC Results

Group: Nate, Chris, Danielle

Two other visualizations that we’ve composed to address this problem use a color encoding to demonstrate the changes in data across different frameworks. Both visualizations utilize a red-blue color ramp encoding the normalized value of the data point. All data elements are pulled from the upper triangle of the matrix, so no redundant information is encoded in the view.

The first is a wheel with each wedge representing an individual matrix in the graph. Each of the rings then represents a single category pairing in the matrix. As a result, comparing the colors around a ring reveals trends in that pairing between the matricies. Comparing colors between rings reveals the relationship between the variable sets. Finally, comparing wedges reveals the similarity between matricies. Eventually, mouse overs should be integrated to give more information about any particular circle segment.

A second visualization, drawing from heat map principles, maps each matrix to a position along the x-axis. A particular pairing is then mapped to the y-axis. Mouseing over a box reveals the raw value represented by that individual data point. In this view, skimming across a row reveals relationships between variables across the matricies. Comparing boxes in the columns demonstrates the patterns within a matrix. Comparing rows represents comparisons between variable pairings. Comparing columns allows the user to compare different matricies.

The third visualization is a kind of console for viewing the eigen-spectrum / PCA properties of the data. This console consists of 5 windows:

– The original data matrix

– The spectrum of eigenvalues

-The original matrix recomposed from the top 3 eigenvectors

-The PCA view of the matrix in 2D

-The first 3 eigenvectors mapped independently to the RGB channels.

A screen capture is shown below.

Team of Jeremy, Adrian and Leslie

A scatter plot matrix of pairwise projections.

This demo is online, and can be viewed here.

This prototype explores the idea of showing every possible axis aligned 2D projection. The weight between the nodes indicates the strength of the paring. In a given scatter plot, the position of the nodes is calculated by using the current two axis as to perform a lower dimensional projection. This allows us to see a difference in shape between each of the frameworks from several different “meaningful” views.

The Group: Danielle, Chris, and Nate.

Here’s one of our sample designs — this shows a difference between two of the practicum datasets:

The pattern of this design is generally to show the data in a matrix layout. At the top of every cell, there’s the value of some comparison metric. At the bottom of the cell, the raw data (or something roughly equivalent) is shown — albeit in a low-res format. In this example, color redundantly encodes the main metric in a heatmap; with more complex comparison metrics, that need not be the case. Additionally, when the comparison metric has some sense of whether this comparison passed some statistical threshold, it can only color those cells that do.

Mouseover (or some other cell selection mechanism) can display additional information about the comparison in question — data values, diagnostic information on the residuals, and such.

Closed radial pattern with the same orientation applied to all samples.

Team of Jeremy, Adrian and Leslie

This demo is online, and can be viewed here.

The concept places all study samples on the same eight spokes and allows the user to select the study and variable by clicking the ‘wedges’  near the center.  Navigational highlights include:

1. Variables for each study are shown when the pointer is over each wedge and lines are then drawn upon mouse-down.

2. If a new variable is selected, which is different than the previously selected variable, the orientation is adjusted so that the current variable is on top.

3. The user can select all four studies by clicking the letters surrounding the spokes.

4. Values can be seen by placing the pointer over and individual dot (data point) and a circle is drawn to show the relative position of other points along other spokes.

5. The play button (which is currently not functional) will be used to animate between different time points in the longitudinal studies.

Team members: Jim Hill, Ye Liu, Shuang Huang

Overview

Our goal is to develop a tool that will answer these two questions.

1. Given a set of frame’s, what is the general distribution of the frames.
2. Given two or more frames, how do they each compare.

To solve the first question we first decided that there must be a way to calculate the distance between two frames.  The method of calculation is not important, how it is visualized is.  We decide to pick a frame as a reference, which frame does not matter.  We then encode the distance of each frame from the reference as the distance of a green circle from the reference frame (red circle) located at the center of the screen.  Frames are spaced evely around the reference frame.  No information is encoded in the frame ordering.  The main window looks like this:

This is an interactive visualization.  Hovering over any of the frames will display it’s name, clicking a frame will select it and double clicking will cause that frame to be used as the reference frame.

After selecting reference frames, clicking the compare button will bring up a compare window in which the frames are directly compared.  We have currently implemented two methods for comparing frames.

Encoding Differences using Lightness

We first find the difference matrix by subtracting one frames elements from the others.  This will result in a set of positive and negative numbers.  To visualize these differences, the size values are encoded using lightness of the color green for positive values and red for negative values.  A very light color represents a very small difference.  A solid green or solid red represents a very large difference.  The following is an image from the comparison:

This method of comparison can only compare two frames.

Encoding Differences using Bars

Our second method of encoding the difference between charts was to create a bar chart for each frame element to be compared.  The visualization still consists of a matrix of boxes, but each box contains a bar chart that shows the relative sizes of each element of each frame.  This allows for more than one frame to be visualized at one time.

Source Code:

Currently this has only been tested on Linux.  It requires linking with the Qt libraries.  The source code can be found at:

http://www.cs.wisc.edu/~jshill4/cs838/DesignChal1/Project

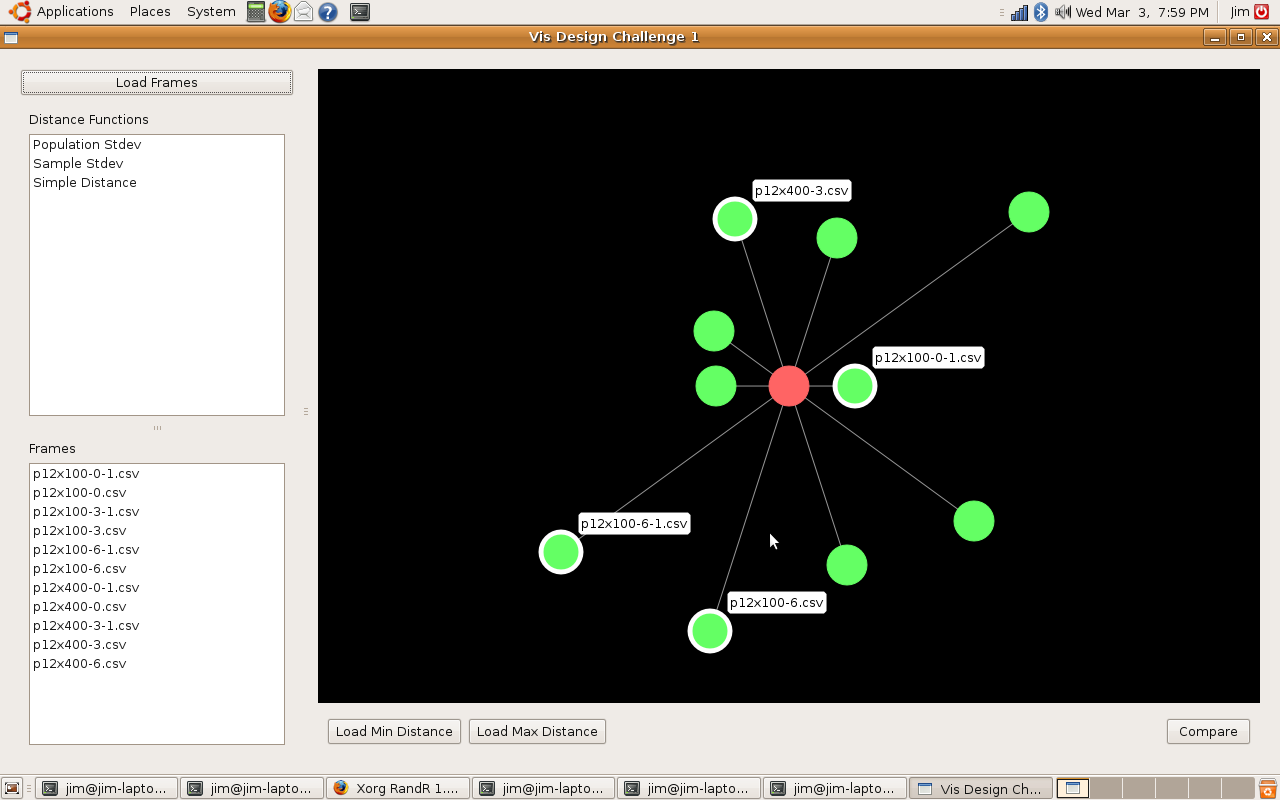
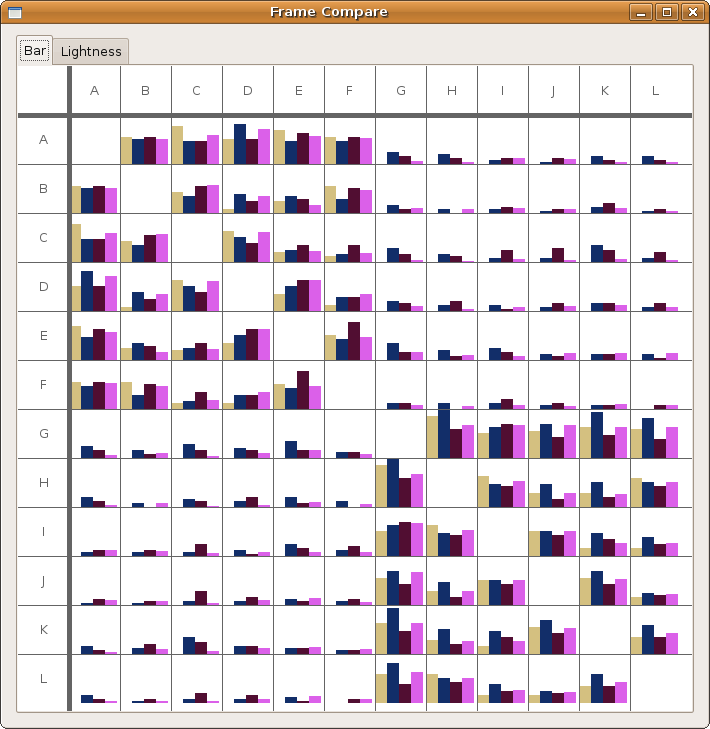
Team: Emma Turetsky, Nakho Kim, Chaman Singh Verma

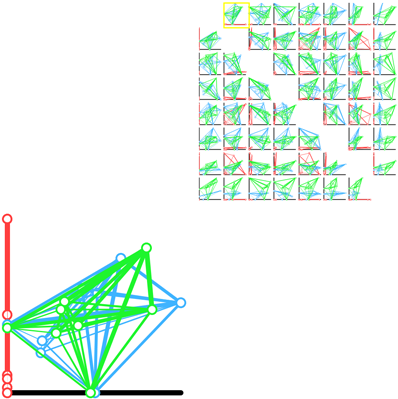
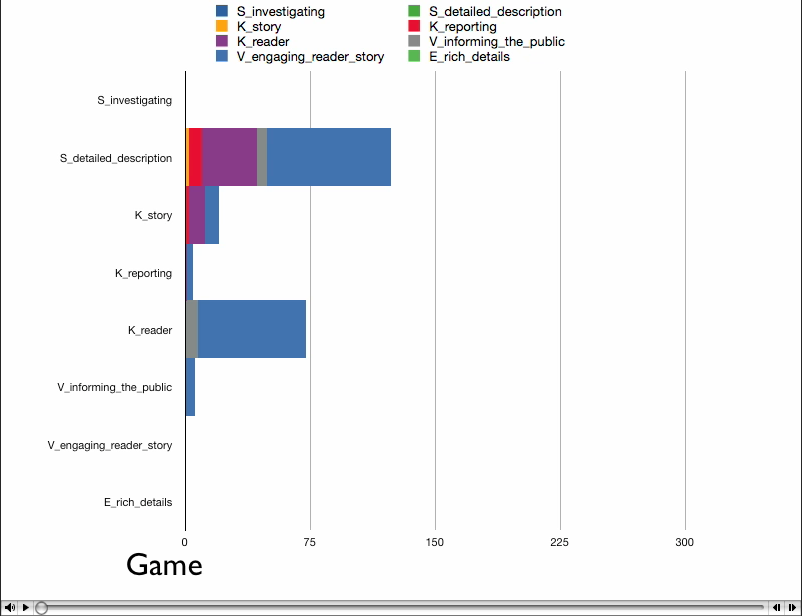
We felt this assignment contained two different problems. One was to get an overall picture or idea of the whole dataset, this would be a general view diagram, the other was to see how one skill or node relates to all the other nodes in the dataset and compare that between two datasets, this would be an egocentric diagram. It is very hard to do both together as it can easily clutter the visualization, making it harder to see the data and make it difficult for patterns to emerge, an example of this is the “spoke graph” the prof. Gleicher’s. So instead, we chose to focus on these problems seperately, rather than trying to do both at one time.

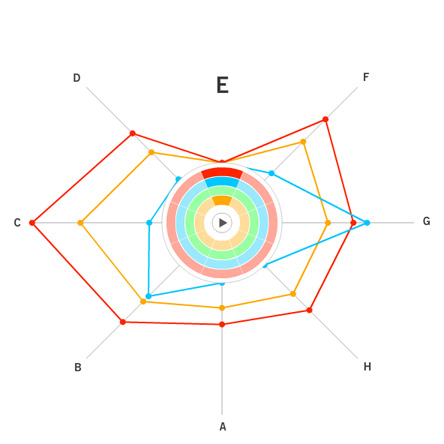
The egocentric approach, which is the one we ultimately chose, is the optimal way for showing individual node connections between one node and the others, but it is hard to show more than one degree of connectedness, making it hard to see the network overall as a whole, even if all the diagrams for the nodes are presented.

One of the major difficulties we saw with this approach was that there was too much clutter, especially around points with low correlation, so we decided to come up with a visualization which reduces the clutter without getting rid of the data completely. We chose a visualization of the second type, one which focuses on how the data relates to one data set, but can be easily compared between datasets.

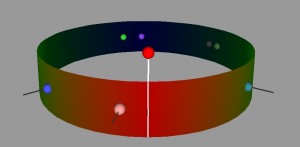
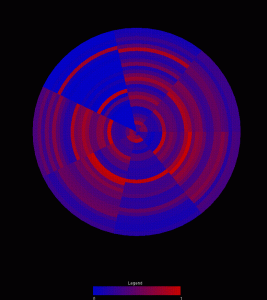
Our visualization is made up of a cylinder. There is a node sticking up vertically from the cylinder, this is the skill/point we are focusing on at the moment. When that point is in the center, you can see one half of the cylinder, the horizontal distance from the main point of the other points on the cylinder represent the correlation. So in this view, the edges of the cylinder are the .5 mark and the point opposite the focused node is 0. Note that this means that distance can be either to the right or the left of the focused point, but direction doesn’t matter. Where a point is vertically on the cylinder also does not matter, but can be used to show multiple points with the same of similar distance without having them overlap. If two points are the same horizontally but different vertically, they still have the same value.

The view can also be rotated so that if you wish to, you can see the points with lesser correlation on the other side of the column. What is nice about this view is that we can display multiple datasets on one column, as long as the focus point is the same. We have also show multiple focus points by stacking the columns on top of each other. While the prototype is not completely finished, we have a program which gives the general idea of what we are trying to achieve.

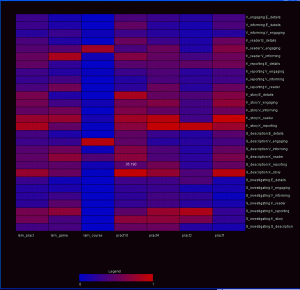
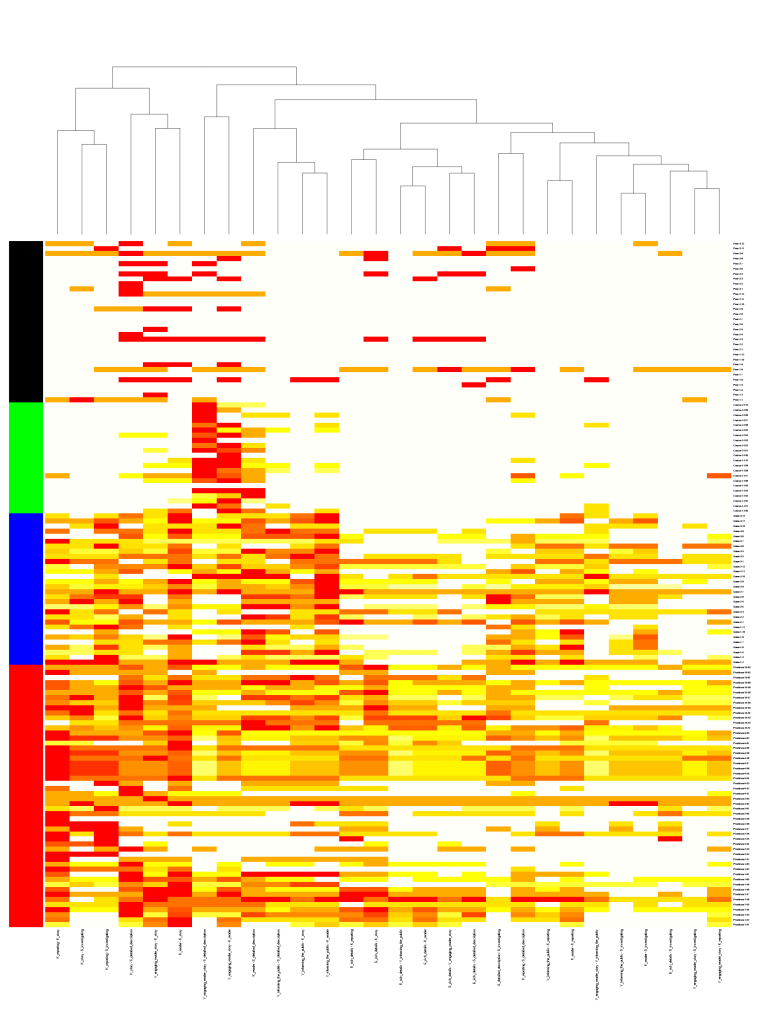
For a general view diagram, the idea is to show the network as a whole. The problem with this is that it gets easily cluttered and makes it hard to read individual connections. In a general view diagram, if the data points hold fixed positions, it’s easy to compare to or more networks, but hard to make a comparison. One example of this is the “golfball” view shown in class. If, in a network diagram, node positions are reordered depending on the dataset, it’s easy to see patterns within one dataset, but extremely difficult to compare between datasets.

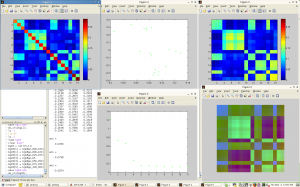
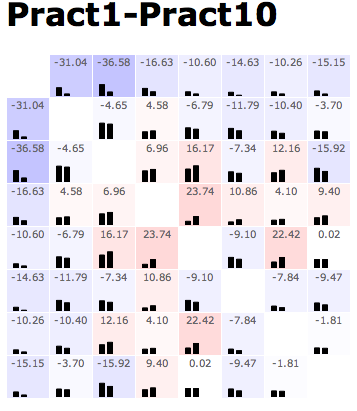
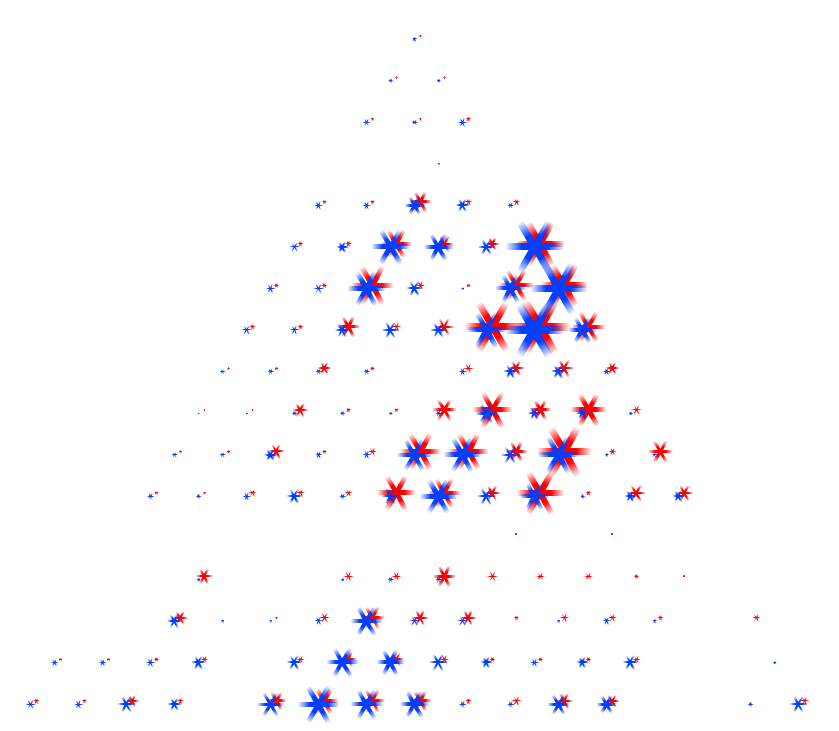
For an overall view, we decoded to use a fixed comparison of data matrices. We did this by essentially using the given matrix as the x and y coordinates in a plot and the correlation as some other value, in this case color. Then we noticed that since the matrices are identical, we could replace one triangle of a matrix with the other to get one graph where the coordinates on one side are symmetric with the coordinates on the other side. Doing this for a wafer plot gives us the following three plots.

Note that while you can clearly tell that the datasets have some differences, it is really hard to see what exactly those differences are. Due to the statistical software used, a gradient is formed, so though the original data on the vertices are distinct points, these plots imply and idea of connection and intermediate points between the data.