Team: Emma Turetsky, Nakho Kim, Chaman Singh Verma
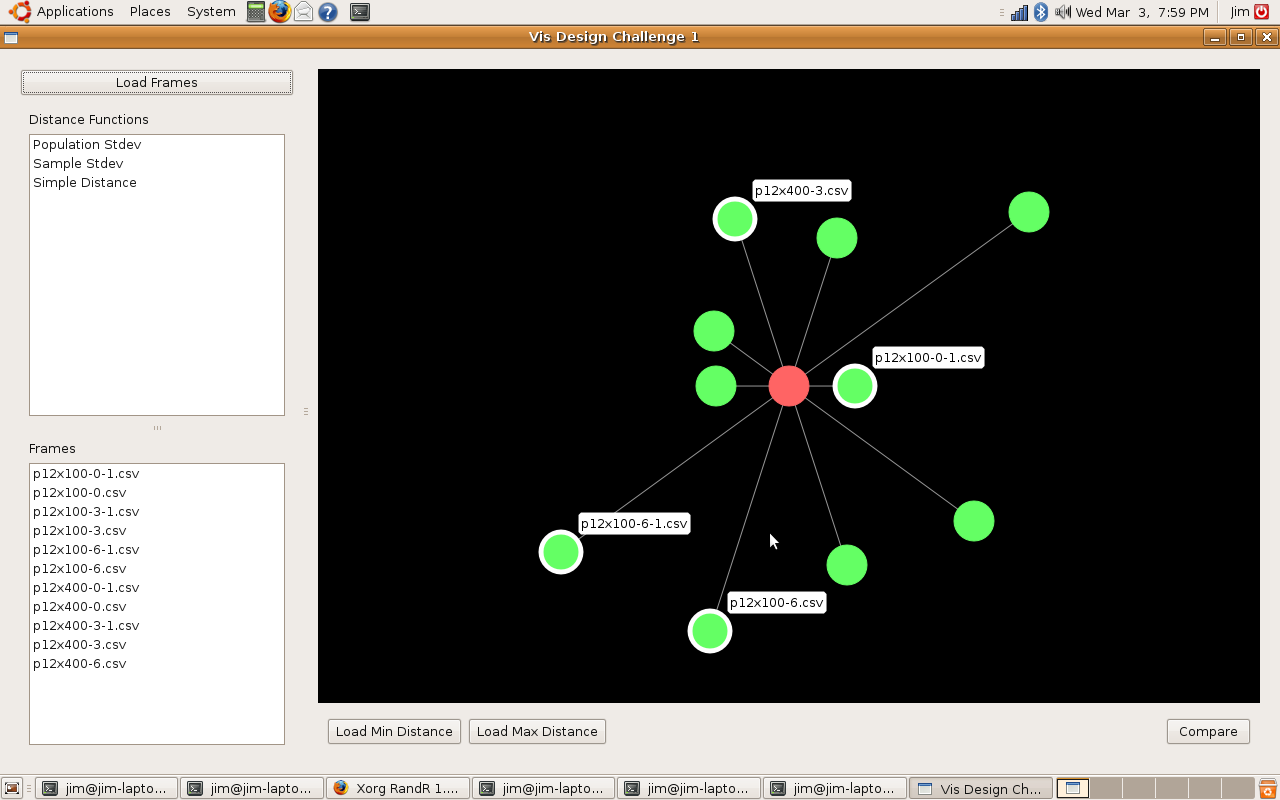
We felt this assignment contained two different problems. One was to get an overall picture or idea of the whole dataset, this would be a general view diagram, the other was to see how one skill or node relates to all the other nodes in the dataset and compare that between two datasets, this would be an egocentric diagram. It is very hard to do both together as it can easily clutter the visualization, making it harder to see the data and make it difficult for patterns to emerge, an example of this is the “spoke graph” the prof. Gleicher’s. So instead, we chose to focus on these problems seperately, rather than trying to do both at one time.
The egocentric approach, which is the one we ultimately chose, is the optimal way for showing individual node connections between one node and the others, but it is hard to show more than one degree of connectedness, making it hard to see the network overall as a whole, even if all the diagrams for the nodes are presented.
One of the major difficulties we saw with this approach was that there was too much clutter, especially around points with low correlation, so we decided to come up with a visualization which reduces the clutter without getting rid of the data completely. We chose a visualization of the second type, one which focuses on how the data relates to one data set, but can be easily compared between datasets.
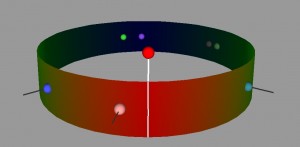
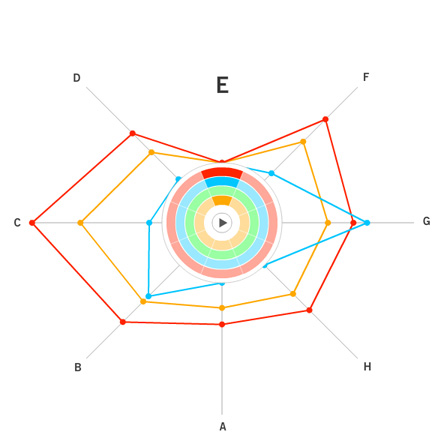
Our visualization is made up of a cylinder. There is a node sticking up vertically from the cylinder, this is the skill/point we are focusing on at the moment. When that point is in the center, you can see one half of the cylinder, the horizontal distance from the main point of the other points on the cylinder represent the correlation. So in this view, the edges of the cylinder are the .5 mark and the point opposite the focused node is 0. Note that this means that distance can be either to the right or the left of the focused point, but direction doesn’t matter. Where a point is vertically on the cylinder also does not matter, but can be used to show multiple points with the same of similar distance without having them overlap. If two points are the same horizontally but different vertically, they still have the same value.
The view can also be rotated so that if you wish to, you can see the points with lesser correlation on the other side of the column. What is nice about this view is that we can display multiple datasets on one column, as long as the focus point is the same. We have also show multiple focus points by stacking the columns on top of each other. While the prototype is not completely finished, we have a program which gives the general idea of what we are trying to achieve.
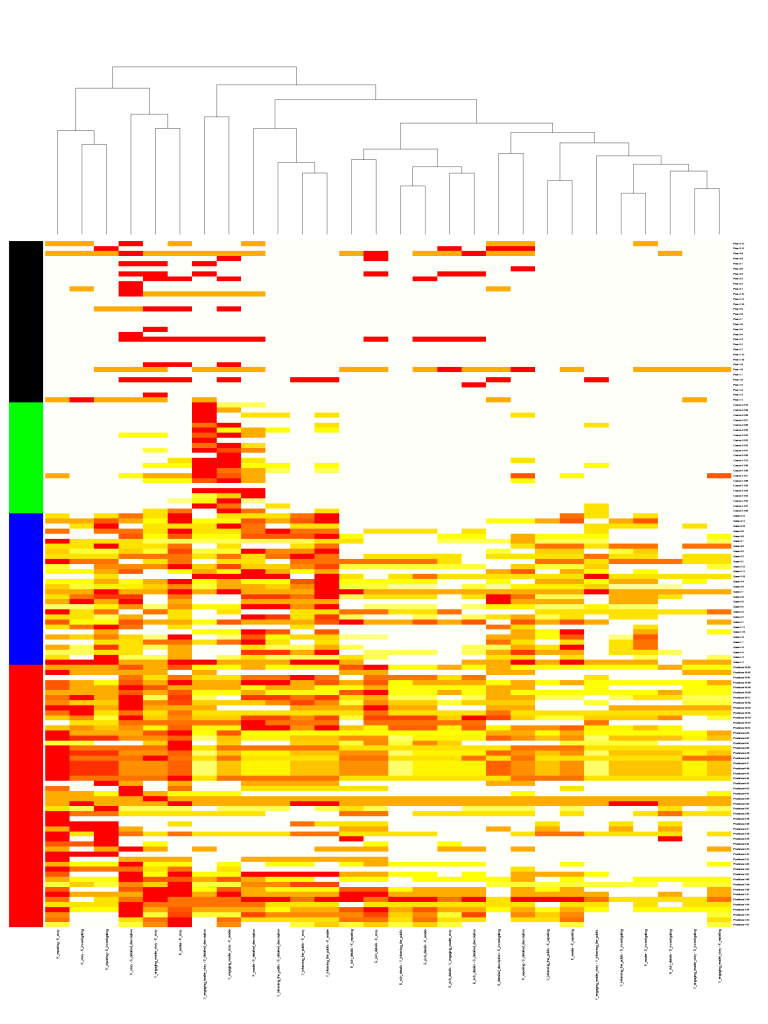
For a general view diagram, the idea is to show the network as a whole. The problem with this is that it gets easily cluttered and makes it hard to read individual connections. In a general view diagram, if the data points hold fixed positions, it’s easy to compare to or more networks, but hard to make a comparison. One example of this is the “golfball” view shown in class. If, in a network diagram, node positions are reordered depending on the dataset, it’s easy to see patterns within one dataset, but extremely difficult to compare between datasets.
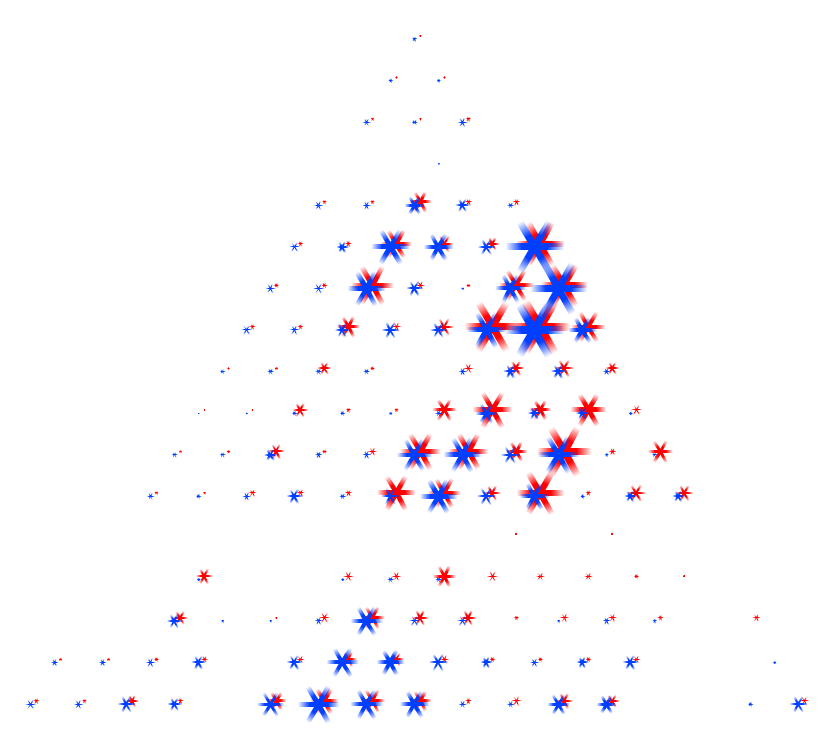
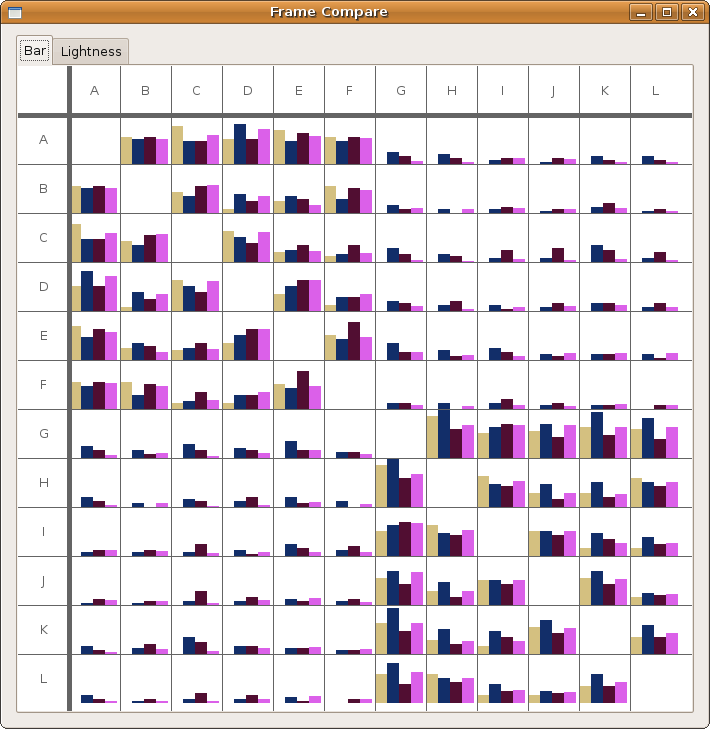
For an overall view, we decoded to use a fixed comparison of data matrices. We did this by essentially using the given matrix as the x and y coordinates in a plot and the correlation as some other value, in this case color. Then we noticed that since the matrices are identical, we could replace one triangle of a matrix with the other to get one graph where the coordinates on one side are symmetric with the coordinates on the other side. Doing this for a wafer plot gives us the following three plots.



Note that while you can clearly tell that the datasets have some differences, it is really hard to see what exactly those differences are. Due to the statistical software used, a gradient is formed, so though the original data on the vertices are distinct points, these plots imply and idea of connection and intermediate points between the data.