Assignment 4

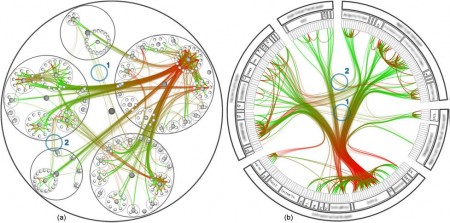
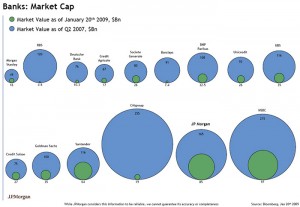
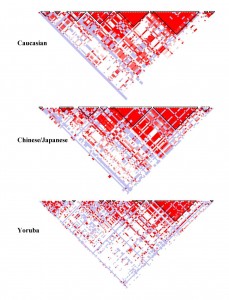
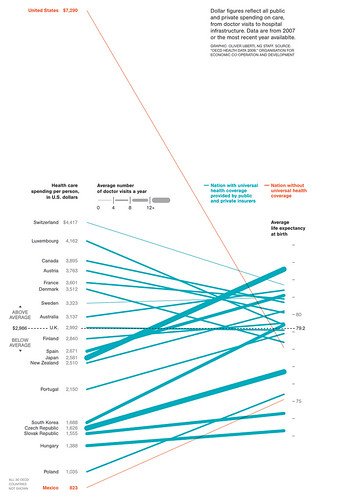
Good

“Who is Paying Taxes” mint.

http://www.mint.com/blog/wp-content/uploads/2009/11/MINT-TAXES-R4.png

Found at: http://www.visualizingeconomics.com/

Critique

The chart above was found at the website cited above and a large version can be found by going there.  This visualization falls on the InfoVis/Present side of the two perspectives covered in class and attempts to show the relation ship between income and income tax payed by different brackets of the population.  The chart would be of interest to any member of the united states curious about who pays what percent of income tax. The chart contains both quantitative and ordered data.  The quantitative data includes income size and percentage of taxable income.  The ordered data includes income levels and percent income tax paid.  I consider percent income tax paid to be ordered data because while the percentages could be considered quantitative, they are displayed in the context of a pie chart in which the size is used to create an ordering.

Tasks enabled include

1. Determining what percentage of the population falls into a certain tax bracket.
2. Determining what percentage of income in each tax bracket is considered taxable.
3. Determining relative sizes of different tax brackets
4. Determining how much total income tax is payed by each tax bracket.

Income size is encoded with plain text for each tax bracket.  Percentage of taxable income is also encoded with text but also with a horizontal bar that is shaded with hash marks over the required percentage.  Income levels are encoded using different shades of the color green with lighter being the lowest and higher being the darkest.  The size of the tax brackets is encoded in the height of the green blocks as well as percentages to the size of the blocks.  The percent income paid is encoded in a pie chart to the right of the income block along with text in each piece giving an exact value and shading that reflects the green counterpart.  Connections are made between each income block and its percent of total income tax with lines that do not intersect.

Ordering of the tax brackets is done using both position and lightness.  The highest earners are at the top and the lowest are at the bottom with the bottom being the lightest and the top being the darkest.  According to Munzner, position is the best encoding for all data types, for ordered data, lightness is the second best encoding.  The second best encoding for quantitative data is length which is used for percent of taxable income, and to some extent percent of income tax paid.  Area is used extensively in both the table and the pie chart.  While this is not one of the best encodings for any of the data types, it does allow the viewer to relate the sizes of two datum.

This visualization makes if very easy to answer the question “what percent of total tax income comes from what tax bracket.”  It is clear that even though only 1.8% of the income of the highest tax bracket is taxable, that bracket still pays the majority of income tax collected.  This is very important because saying that only 1.8% of income is taxable for those making more than $500,000 per year could be very misleading.

This is also a good example of removing chart junk.  There are no tidbits of information cluttering the valuable information.  There is a proper title and narrative at the top and a signature at the bottom.  The rest is information relevant to the visualization.

Bad

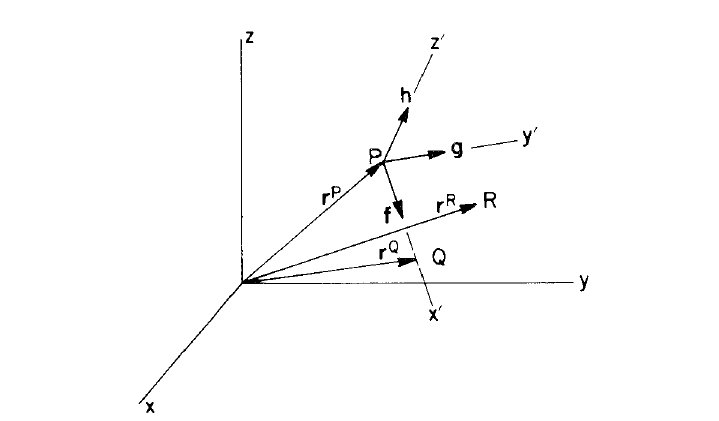
Edward J. Haug. Computer Aided Kinematics and Dynamics of Mechanical Systems. Allyn and Bacon 1989

Critique

Visualizations of three dimensional spaces occur in almost every graphics and vector-math text book.  The image above is only an example of how this visualization is attempted.  The example image is attempting to show a local reference frame inside of a global reference frame and depict points in each.  This visualization method fails because often it doesn’t provide any method for determining “true” orientations.  Often these visualizations are given as an afterthought to a larger more thorough narrative, however, even with a good explanation, the visual can be misleading.  The main issues is that one entire dimension worth of data is thrown away in order to present the data in a two dimensional form.

There are a number of ambiguities including what direction is the x axis of the global reference frame pointing?  Are z’ and x’ pointing towards or away from the viewer?  Where is R?  With a little information including knowledge of left or right handed conventions, these questions are a little easier to answer however there are a number of queues that could be added to help pull useful information from the image

This is a graph that compares the market values of various banks at two different times. Once in 2007, the other after the crash to show value in early January, 2009.

This graph is very misleading, shape is probably not the best method to display the data, especially when there are only two pieces of data that are being compared within one bank. If the plan is to also compare between different banks, then there should be a better ordering, possibly by original market value (represented by the blue circles) or changed market value (represented by the green circles), depending on what you wish to show or compare.

One major problem with this image is that I quantify and compare areas much more readily than I do diameter, which is how the circle sizes are determined. Especially as there is no actual diameter lines written in to compare the two. For example, Goldman Sachs, which has dropped from 100 to 35, does not immediately appear to be worth about a third of it’s original value. Looking at the graph, my first impressions is that it’s worth a much smaller fraction of the value. This is a very misleading image.

I think this is an elegant way of displaying connections between a huge dataset.  To explain, this is a haplotype map that has SNPs (single nucleotide polymorphism) at the top (where it is feathered). They then study the genes of a population to determine the probability that SNPs occur together (called linkage disequilibrium. If you take two white squares at the top, and then draw lines parallel to the triangle to get an intersection, you get a square that represents that probability. A higher probability (closer to 1) is colored red. A probability that approaches random (.5) is white, with blue being slightly better than random and light red being between red and blue.

This means that triangles of mostly red, which are marked off in these plots, are those SNPs which are more likely to be passed on together during chromosome crossover. In the Caucasian sample, there are many more of these than in the Yoruba sample, which implies that any mutation that added something new to the gene pool happened more recently for Caucasians than Yoruba, as more crossovers (more generations) means less linkage disequilibrium.

These graphs are specifically of chromosome 8p23.1 and is for a 100kb region.

The intended audience are those with an understanding of biology and the human genome. It allows you to see, at a glance, genes or SNPs which are connected. This encodes probability to color, and uses position as a way of filling in the matrix connecting two values. The positions along the top of the triangle is mapped to position in the chromosome itself. I think it is good because you can clearly see the connections between different SNPs and regions with are likely to stick together during the recombination required to create gametes. It also is simple to glance between different HapMaps of the same chromosome in different populations and see which has had the most recent mutation (and therefore less time to be more random in the population).

The Cost of Care

http://blogs.ngm.com/blog_central/2009/12/the-cost-of-care.html

This visualization compares cost of healthcare per person to average life expectancy for various developed countries. This text is included on article linking to the actual image:

“The United States spends more on medical care per person than any country, yet life expectancy is shorter than in most other developed nations and many developing ones. Lack of health insurance is a factor in life span and contributes to an estimated 45,000 deaths a year. Why the high cost? The U.S. has a fee-for-service system—paying medical providers piecemeal for appointments, surgery, and the like. That can lead to unneeded treatment that doesn’t reliably improve a patient’s health. Says Gerard Anderson, a professor at Johns Hopkins Bloomberg School of Public Health who studies health insurance worldwide, “More care does not necessarily mean better care.”  —Michelle Andrews “

This visualization encodes four dimensions of data in the following ways:

–       Cost of healthcare per person- y position

–       Average life expectancy- y position

–       Average number of doctor’s visits per person- line thickness

–       Type of coverage (universal or otherwise)- hue

What Munzner might say:

Cost and life expectancy clearly fall into the quantitative data category, and are encoded using position, the strongest visual channel for their data type. Type of coverage is categorical, and is encoded using hue, the second strongest visual channel for its data type (after position, which has already been used).  All the visual channels are seperable, and code these four dimensions without confusion. Also, cost and life expectancy are connected by lines, so their relationship is encoded using line slope. Clearly and explicitly relating this data makes the US pop out as the country with the steepest downward slope.

What Tufte might say:

First, this graphic is well documented. The creator, his position, the data source, the year the data was collected, the fact that some countries aren’t shown, and the scales for all the numeric data are all clearly written on the image. The lines connecting cost and life expectancy facilitate clear comparisons of all the data.

Edit: Here’s an interesting article where the creator justifies his design choice over a scatterplot: http://blogs.ngm.com/blog_central/2010/01/the-other-health-care-debate-lines-vs-scatterplot.html

Trends and Technology Timeline 2010+: A roadmap for the exploration of current and future trends

http://nowandnext.com/PDF/trends_and_technology_timeline_2010.pdf

This visualization denotes current trends as well as predictions for future trends, and displays them in a way that is analogous to a subway map. This text is included on the map:

“This map is a broad representation of some of the trends and technologies currently visible. Improvement works are carried out at weekends and travellers should check to see whether lines are still operable before commencing any journeys. Helpful suggestions concerning new routes and excursions are always welcome.”

This visualization encodes five dimensions of data in the following ways:

–       “time zones”– radial distance from the center of the map, hue

–       phenomena – text labels, position on category lines, connection?

–       category of phenomena – hue

–       type of phenomena – shape, glyphs

–       global risks – bulleted list, containment?

What Munzner might say:

First of all, this “roadmap” doesn’t even use the strongest visual channel(s): absolute x and y position. Then, it uses hue to distinguish different time zones (even though this is ordered data, and saturation would be more appropriate), AND to distinguish different categories. And there are 16 different colors corresponding to different categories, even though the max amount of colors used should be eight.

What Tufte might say:

What is meant by “time zones”? The common definition of this word is very different from the definition as relates to this visualization. Also, trends appear on category lines in a particular order. Is there any logic behind this order? Does it imply causality? Finally, the extremely dense text doesn’t make very judicious use of ink.

The problem of displaying a data set that is multi-variate, time-varying, and comparative in nature is inherently very difficult. Jonathan Woodring and Han-Wei Shen at Ohio State have developed a very aesthetically pleasing method of displaying such information using three dimensional color mapping. However, their solution leaves a lot to be desired in terms of the composition of a successful visualization. While the colors do make for very visually pleasing images, the visualizations themselves are very difficult to interpret. The value of any given data point is encoded in its color and its position is representative of its relation to other data collections as defined by a set vocabulary of logical operations that the tool can visualize (over, in, out, atop, and xor). In addition to the limitation on the amount of data that is provided, the visualization provides the user with neither manner of inferring what the values encoded by the color actually represent nor a physical representation of the meaning of the positioning coordinates. Essentially, the user has no manner of extracting any data out of the visualization other than two points being different over one dimension or another. A user simply looking at the output of this visualization cannot really gain much from the end result other than a pretty picture generated from a complex data set. This visualization technique seems to have potential, but in it’s current state, it is simply not a very useful mechanism for data comparison.

Above is an image of a visualization generated by this tool representing a logical combination of data points from the Supernova Initiative Data Set. The paper and additional images can be found here.