A first attempt at LSA (Latent Semantic Analysis)
LSA is an older corpus processing method – it’s kind of gone out of favor for things like topic modeling – but I like it as an illustration because it is very simple. And to use it, we have to make all the critical decisions we need to do with any statistical modeling thing. And of course, simple experiments are good for exposing errors in our data and process (fixes were made to my code in the process of doing this, but the data is standing up).
LSA is basically performing PCA on the word count vectors. So, it has all the problems of both (it only considers word counts, and its only looking for variance).
First, I need to pick which documents. You might say “that’s easy – use all of EEBO-TCP,” but since I know there are things in the corpus that might throw me off, I might as well cull things first.
For now, I’ll first remove all documents for which our metadata tells us the document is not in English (since I am interested in English). And I’ll remove all documents shorter than 250 words (that number is arbitrary) – since if documents are too short normalization might get weird. (If a document is 5 words long, then each word is 20% of it.) Note these are arbitrary choices – they affect the results, and I should remember that I did them. But it would be appropriate to make different choices.
My data is now a 52049 x 6065951 matrix of 52049 documents in EEBO-TCP that are in English and long enough, 6065951 words to be counted – although this is the number in the whole of TCP since I didn’t remove the words that only appear in this corpus). I could remove words that don’t appear a lot – this is a good idea if for no other reason that it makes things go faster (dealing with 6 million columns takes time). It also helps because the small values for uncommon words not only won’t matter in the answers (since the goal is to find the big trends), and that these small values can actually mess things up.
So, I’ll as a next step get rid of uncommon words. There are many ways to do this – for now, I’ll only allow words that appear in 10 or more documents. That’s still a lot of words (447215).
As a sanity check, I can see if any documents are severely affected by this by seeing what document has the lowest percentage of words that remain after removing those words that occur in 10 or fewer documents. The worst document only retains 58% of its words (it’s A12751, “‘A brief treatise for the measuring of glass, board, timber, or stone, square or round being performed only by simple addition and substraction, and that in whole numbers, with[o]ut any multiplication, or division at all / by John Speidell …” which has a huge table of numbers at the end.
If you’re curious, on my (relatively fast with lots of memory) computer, it takes 132 seconds to run LSA (for 20 vectors – I’ll explain in a moment) on the whole massive matrix, on the reduced (10 or more documents), it takes 56 seconds (about half). In case you’re wondering… this isn’t too surprising. Since those rare words were so rare, the computations were smart enough not to waste much time on them.
What can we learn from this first model?
LSA (or at least my implementation) of it is a little different than PCA in that I don’t mean center things before analyzing the matrix. This difference is small, since the mean comes out as the first component – but it can lead to other subtle differences.
The zeroth component is a vector that says “if you could pick only one vector to make the books” (each book is a scaled amount of this vector) which should you pick? The right answer is to pick the average book. So we’d expect that the zeroth vector to be proportional to the average over the books. So the most common words come out as the “strongest” in this vector. While the vector is big (it has a value for each of 447215 words), we can just look at the biggest entries:
[('the', 0.61865592352172205),
('of', 0.40348356075050867),
('and', 0.38341452460366676),
('to', 0.26211624561016428),
('in', 0.18697302248166897),
('that', 0.1653677553047907),
('a', 0.13252050497989859),
('is', 0.11119574845880302),
('it', 0.10087079005559051),
('he', 0.097740434591416875)\
What this tells us is that if you we want to describe books (or their word vectors) with 1 number, this is the best vector to multiply that number by.
Usually, with PCA we ask about the documents. But here, it won’t tell us much: it will mainly tell us how long the books are. Since our book vectors are word counts, longer books will use more of the “average” stuff. The number with the biggest amount is the longest document.
But, if a document is weird (unlike the average) it might use more or less than you’d expect given how long it is. So we could normalize by the document length. Documents that score low on this are ones that don’t use the common words as much as you would expect (given their lengths). The document with the lowest score? A64613… ‘An useful table for all uictuallers & others dealing in beer & ale’ – which is a big table of numbers.
So before doing PCA/LSA we need to normalize for the length of the books. I will do this by dividing each row of the matrix by the length of the book in words (the L1 norm) – using the word count BEFORE we threw out uncommon words.
So now I am building my first “real” LSA model: I chose EEBO-TCP documents that I know to be in English, only considered documents with more than 250 words, and am normalizing the the original word count of the document.
The zeroth vector is actually slightly different – suggesting that long documents use different proportions of words, although this isn’t necessarily something meaningful or statistically significant.
[('the', 0.59010211288364689),
('and', 0.42698349761656479),
('of', 0.39453632948464623),
('to', 0.28559405040930685),
('in', 0.18348404712929461),
('that', 0.15612291442776627),
('a', 0.13154084693700221),
('be', 0.10011301035536961),
('is', 0.097944973306089519),
('for', 0.096814220825602454)]
Again, this is just the top 10 words.
When I look at documents that are “strong” in this vector, its documents that are made up more common words than normal (with a big weighting on “the”). Here are the top few…
A28654 0.1983 A plain and easy rule to rigge any ship by the ...
A96930 0.1813 The use of the universal ring-dial.
B05531 0.1789 Proclamation anent the rendezvouses of the militia...
B04164 0.1780 Londons ordinary: or, Every man in his humor...
A92666 0.1768 A proclamation anent the rendezvouses of the militi...
B24252 0.1765 An explanation of Mr. Gunter's quadrant, as it ...
A72802 0.1764 Londons ordinary, or every man in his humor To ...
A66689 0.1764 To the Most Excellent Majesty of James the IId ...
A01661 0.1761 This book does create all of the best waters ...
B05530 0.1748 Proclamation anent the rendezvous of the militia, ...
That first one has a lot of “the” in it (as expected). I didn’t check the others, but there seems to be a theme.
If we look at the bottom scorers, we see books that don’t have many common words…
A64613 0.0034 An useful table for all uictuallers & others dealing in beer & ale
A28791 0.0039 A Book of the valuations of all the ecclesiastical preferments in England and Wa
A61096 0.0045 Villare Anglicum, or, A view of the towns of England collected by the appointmen
A88337 0.0062 A list of the imprisoned and secluded Members.
A28785 0.0067 A Book of the names of all parishes, market towns, villages, hamlets, and smalle
A95633 0.0068 A table of excise for strong beer and ale, for common brewers at 3s. 3d. the bar
B09789 0.0081 A list of the English captives taken by the pirates of Argier, made public for t
A95631 0.0082 A table of excise for small beer for common brewers at 9 d. the barrel, with the
A28887 0.0082 An exact alphabetical catalogue of all that have taken the degree of Doctor of P
A48671 0.0082 A list of the names and sums of all the new subscribers for enlarging the capita
Again, not surprising… these are books of lists (so they have no need for many articles).
Now if we look at the next principle vector (the 1st LSA vector – since the previous was the zeroth) we would expect to see the words where we have the most variance from the average. Since words that occur often will vary a lot in how often they occur (a small percentage of variance in a common word is still a lot of variation), we expect to see them again. And we do:
[('the', 0.38420645622523014),
('of', 0.32922762730011762),
('your', -0.084669152332760914),
('his', -0.088128326440172142),
('so', -0.089329190198924976),
('with', -0.092148634300003029),
('for', -0.1008359401690339),
('will', -0.11693098516660286),
('me', -0.11984594738903771),
('not', -0.14030401361190545),
('but', -0.14408743558833309),
('it', -0.15588034041694304),
('that', -0.16401056893070368),
('is', -0.17369018634007896),
('he', -0.1772685229064182),
('you', -0.18990955717829638),
('my', -0.19381100534134885),
('to', -0.22065219350754178),
('a', -0.25761137977106813),
('i', -0.37919606548968343)\
What’s interesting here – “the” and “of” are on top, and words that are more personal are at the bottom. If you’re writing a lot about yourself or people, you don’t use as many definite articles. If you write about “the X of Y” a lot, you aren’t going to say much about “I, you, …” So the top on this list is book that are declaring facts:
A28654 0.1152 A plain and easy rule to rigge any ship by the length of his masts, and yards, w
A66689 0.1107 To the Most Excellent Majesty of James the IId by the grace of God of England, S
A18462 0.1027 The Imperial acheiuement of our dread sovereign King Charles together with ye ar
B05531 0.0921 Proclamation anent the rendezvouses of the militia, for the year 1683.
A92666 0.0907 A proclamation anent the rendezvouses of the militia, for the year 1683; Proclam
B05530 0.0900 Proclamation anent the rendezvous of the militia, for the year, 1684.
A93594 0.0886 A survey of the microcosme. Or the anatomy of the bodies of man and woman wherei
A93593 0.0866 An exact survey of the microcosmus or little world being an anatomy, of the bodi
A39982 0.0844 The form of the proceeding to the coronation of Their Majesty's, King James the
B03350 0.0830 The form of the proceeding to the coronation of their Majesty's, King James the
And the bottom?
B01741 -0.0804 Tobia's advice, or, A remedy for a ranting young man. While you are single you t
A75449 -0.0744 An Answer to unconstant William, or, The Young-man's resolution to pay the young
B00386 -0.0733 A new ditty: of a lover, tossed hither and th\[i\]ther, that cannot speak his mind
A15699 -0.0726 The honest vvooer his mind expressing in plain and few terms, by which to his mi
B01734 -0.0713 Doubtful Robin; or, Constant Nanny. A new ballad. Tune of, Would you be a man of
A06395 -0.0712 The lovers dream who sleeping, thought he did embrace his love, which when he wa
B00382 -0.0712 The lovers dream: who sleeping, thought he did embrace his love, which when he w
B02419 -0.0712 The country-mans care in choosing a wife: or, A young bachelor hard to be please
B04151 -0.0710 The London lasses lamentation: or, Her fear she should never be married. To the
B02416 -0.0708 The country lovers conquest. In winning a coy lass ..., To a pleasant new tune,
Notice that this is all based on the most common words – they will drown out all the uncommon words.
Usually in modeling (like LSA), we get rid of the common words. Here, we can use them to learn things about the corpus and to help organize it.
Of course, with a PCA like thing, the first thing someone wants is a scatterplot. With 50,000+ points, it’s a blotch. In time, we need some interactivity. You can identify the extreme points from the lists above.
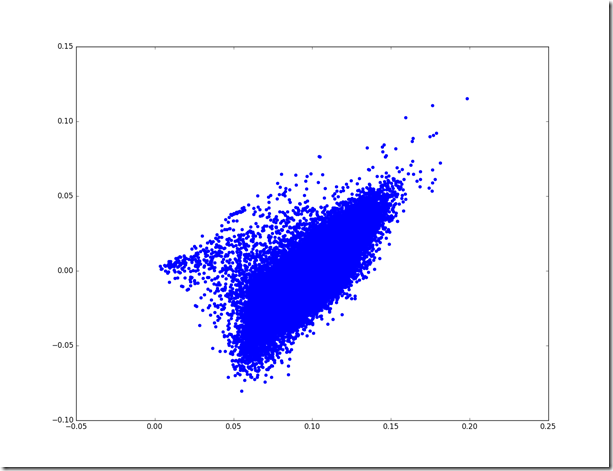
Let’s try to understand why PCA puts “the” and “of” together. Here’s a similar plot of “the” on the X axis and “of” on the Y.
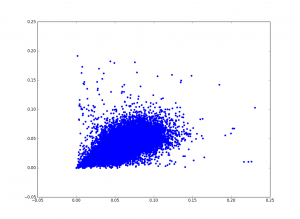
Not hugely correlated (it’s hard to see with the density). But compare that to a plot of “the” vs. “i”:
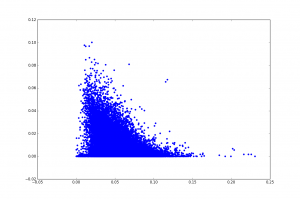
This is pretty striking, because there are many documents that don’t use “i” at all. And some that use I a lot. Yes, there is a document where 10% of the words are I!
A75449 0.1002 An Answer to unconstant William, ...
B03187 0.0977 An excellent new song, called, ...
B04151 0.0970 The London lasses lamentation: or, ...
A73881 0.0968 A Sweet and pleasant sonet, entitled, ...
B00386 0.0867 A new ditty: of a lover, tossed hither ...
B06543 0.0852 Where Helen lies. To an excellent new ...
Or a document that is nearly 20% “of”!
A75823 0.1917 An Account of what captives has been ...
A38857 0.1825 An exact account of the number of ...
A92491 0.1809 Act for raising four months supply. ...
A31306 0.1798 A Catalogue of the prelates and clergy ...
A38907 0.1734 An Exact catalogue of the names of ...
Can these kinds of analysis of common words tell us anything about thelarge corpora?
Let’s try the words/not words game again…
This time I will start with the entire TCP corpus (61315 documents – this includes some Evans and some ECCO). There are 6065951 different words (which is a lot – it gives us a 61315×6065951 matrix). But most words occur once in the whole corpus. I’ll limit things to words that appear in 5 or more documents (there are still 909665 words). Also here I am referring to different words (e.g. “the” counts once) – the total “word count” is 1,541,992,473 (e.g. “the” occurs 89821184 times).
For my subset, I’ll take the drama collection. While there are 1244 plays in the Extended Drama 1700 corpus, there are only 1020 TCP entries (since many plays are in multi-play volumes). Note that I am using entire TCP files for this experiment (so if there is some non-plays mixed in with the plays, I am counting that).
The plays represent 1.56% of the TCP (in terms of word count, after throwing out words that appear in fewer than 5 documents).
Now we can play our words/notwords game… What words are used most in plays (relative to their total usage).
Spoiler alert: I am not going to find too much that’s interesting…
It turns out that there are 32 words that are used only in plays (and remember, this means 5 or more plays, since we excluded words that occur in fewer than 5 documents).
[(1.0, 18, 37, 'foot-marshal'),
(1.0, 9, 41, 'dsdeath'),
(1.0, 9, 17, 'budg-batchelors'),
(1.0, 9, 9, 'three-crane-wharf'),
(1.0, 8, 30, 'dslife'),
(1.0, 8, 18, 'yfayth'),
(1.0, 8, 8, 'theater-royal'),
(1.0, 7, 10, 'waiting-womans'),
(1.0, 7, 8, 'shoulder-scarf'),
(1.0, 7, 7, 'prithe^'),
(1.0, 7, 7, 'exennt'),
(1.0, 6, 12, 'ownds'),
(1.0, 6, 11, 'wudst'),
(1.0, 6, 11, "shan'not"),
(1.0, 6, 9, 'pellited'),
(1.0, 6, 7, 'whooh'),
(1.0, 6, 6, 'skin-coate'),
(1.0, 6, 6, 'bawdship'),
(1.0, 5, 50, 'lucind'),
(1.0, 5, 8, 'undisguises'),
(1.0, 5, 7, "yow'le"),
(1.0, 5, 7, "deserve'em"),
(1.0, 5, 6, 'skirvy'),
(1.0, 5, 6, 'fackings'),
(1.0, 5, 5, 'y^aith'),
(1.0, 5, 5, 'theatre-royall'),
(1.0, 5, 5, "th'help"),
(1.0, 5, 5, 'i\*th'),
(1.0, 5, 5, "hee'de"),
(1.0, 5, 5, 'faintst'),
(1.0, 5, 5, 'drawes'),
(1.0, 5, 5, 'black-fryers-stairs')]
The most common words that don’t appear in plays? The numbers are not a surprise. “Abovementioned” is interesting (and makes sense).
[(0.0, 3884, 20419, 'hebr'),
(0.0, 3809, 12209, 'hezekiah'),
(0.0, 3621, 15286, 'ezra'),
(0.0, 3427, 12124, '3.16'),
(0.0, 3291, 11042, '1.5'),
(0.0, 3250, 9704, '2.3'),
(0.0, 3224, 10329, '2.2'),
(0.0, 3220, 8945, 'abovementioned'),
(0.0, 3179, 10275, '3.1'),
(0.0, 3119, 10031, '3.5'),
(0.0, 3102, 24106, 'esa'),
(0.0, 3097, 9560, '2.1'),
(0.0, 3038, 8862, '2.4'),
(0.0, 3020, 8639, '2.13'),
(0.0, 3008, 7163, 'long-suffering'),
(0.0, 2980, 7576, 'micah'),
(0.0, 2972, 8629, '3.2'),
(0.0, 2966, 8331, '3.8'),
(0.0, 2965, 8506, '3.15'),
(0.0, 2963, 8884, '2.10')]
To get something more meaningful, let’s limit ourselves to words that appear in many plays, but not many non-plays. Here I limit us to words that occur 20 or more times:
[(0.98181818181818181, 28, 55, 'dyes'),
(0.97959183673469385, 37, 98, 'sfoote'),
(0.9666203059805285, 22, 719, 'iord'),
(0.9322709163346613, 28, 251, 'eup'),
(0.92708333333333337, 33, 96, 'vmh'),
(0.92564102564102568, 33, 390, 'iph'),
(0.92356687898089174, 33, 157, 'wonot'),
(0.92307692307692313, 31, 78, 'shannot'),
(0.89333333333333331, 35, 75, "s'foot"),
(0.88741721854304634, 28, 302, 'borg')]
(A reminder, this means that “borg” appears 302 times in TCP across 28 documents. 88.7% of those 302 times are in plays.)
At the other end of the list, we get words that appear a lot in non-plays, but not much in plays:
[(4.3112739814615219e-05, 5121, 23195, 'eccl'),
(4.2984869325997249e-05, 3739, 23264, 'isai'),
(4.0666937779585194e-05, 150, 24590, 'chwi'),
(4.0412204485754696e-05, 6211, 24745, 'isaiah'),
(3.389141191622043e-05, 165, 29506, 'wrth'),
(2.5357541332792372e-05, 185, 39436, 'hyn'),
(2.5131942699170645e-05, 137, 39790, 'efe'),
(2.2714366837024417e-05, 6829, 44025, 'sanctification'),
(2.0277805941397142e-05, 135, 49315, "a'r"),
(1.1377793959529188e-05, 328, 175781, 'yr')]
As a check, the word “the” has .825% of its occurrences appearing in plays. This is about half of what we might expect (since the plays are 1.5% of the words). In contrast, “a” is 1.9% (or higher than expectation).
An experiment we often talk about is to see what words are “unique” to Shakespeare (or some other author, or group of book), and words that are conspicuously missing (e.g. they are very common in the rest of the corpus).
I think this is more an exercise to test our data (especially the standardization) than it is to shed new light on the corpus, but it is still worthwhile.
I start with a corpus (in this case, it’s the “all drama” or 1292 set). I pick a subset (in this case “the 38 plays that have Shakespeare as an author”). I then ask “what percentage of the occurrences of each word is in the subset”. So, if it’s 100%, then all the words are in the subset (in this case, Shakespeare was the only author to use the word), if it’s zero, only texts not in the subset use the word (in this case, Shakespeare never used the word).
I then sort the list by the number of documents it appears in.
This can be really useful for spotting errors – when we tried this with a draft version of the standardization (using VARD), it said that “john” was the most common word Shakespeare never used – something even I knew had to be wrong.
Here are the most common (in terms of number of plays it occurs in) words that Shakespeare does not use:
[(0.0, 461, 1214, 'designed'),
(0.0, 384, 645, 'invite'),
(0.0, 370, 1055, 'however'),
(0.0, 352, 840, 'oblige'),
(0.0, 304, 618, 'sufferings'),
(0.0, 277, 534, 'ills'),
(0.0, 276, 579, 'whatever'),
(0.0, 264, 423, 'various'),
(0.0, 252, 377, 'secured'),
(0.0, 239, 391, 'contrive'),
(0.0, 234, 343, 'numerous'),
(0.0, 232, 2028, 'mrs'),
(0.0, 229, 324, 'conveyed'),
(0.0, 225, 344, 'heretofore'),
(0.0, 225, 283, 'delude'),
(0.0, 224, 599, 'coxcomb'),
(0.0, 214, 290, 'propitious'),
(0.0, 213, 453, 'matrimony'),
(0.0, 211, 314, 'declared'),
(0.0, 203, 272, 'brighter')]
The way to read this: the word “designed” appeared in 461 documents in the corpus, it appeared 1214 times, and 0% of these were in the 38 plays that list Shakespeare as an author.
I have a hard time believing that Shakespeare never used some of these words. Could these be symptoms of a standardization issue?
Here are the 20 most common words that Shakespeare used that no one else did
[(1.0, 7, 8, 'sequent'),
(1.0, 5, 11, 'prayres'),
(1.0, 5, 11, "didd'st"),
(1.0, 4, 29, 'bardolfe'),
(1.0, 4, 24, 'glouster'),
(1.0, 4, 10, 'come-on'),
(1.0, 4, 8, 'porpentine'),
(1.0, 4, 5, 'leaue-taking'),
(1.0, 4, 4, 'winnowed'),
(1.0, 4, 4, 'vnfirme'),
(1.0, 4, 4, 'out-stretcht'),
(1.0, 4, 4, 'non-pareill'),
(1.0, 3, 22, 'rosaline'),
(1.0, 3, 12, 'thisbie'),
(1.0, 3, 12, 'glousters'),
(1.0, 3, 9, 'faulconbridge'),
(1.0, 3, 6, 'falstaffes'),
(1.0, 3, 5, 'wildenesse'),
(1.0, 3, 4, 'bawcock'),
(1.0, 3, 4, 'acorne')]
If we go deeper into the list (things that occur in only 1 book) we start to see things like character names.
In this list, we definitely see some standardization issues. For example, “acorne” is not standardized to “acorn” because it wasn’t a common enough word to be considered when we made the standardizer dictionary. Leaue-taking, prayres, vnfirme are also obvious examples of words that would by standardized by an encyclopedic standardizer.
Other parts of the list can also be interesting. Here is the bottom of the list Shakespeare used (the words with the lowest percentages):
[(0.0016168148746968471, 419, 3711, "don't"),
(0.0015408320493066256, 179, 1298, 'gad'),
(0.0014005602240896359, 359, 714, 'treat'),
(0.0013192612137203166, 339, 758, 'concerned'),
(0.0012300123001230013, 45, 813, 'ego'),
(0.0011534025374855825, 321, 867, 'st'),
(0.0010834236186348862, 418, 923, 'fain'),
(0.00099601593625498006, 376, 1004, 'obliged'),
(0.00072358900144717795, 83, 1382, 'j'),
(0.00051334702258726901, 706, 3896, 'its')]
Shakespeare represents 3.9% of the corpus (in terms of word count – it’s about 3% in terms of number of documents). So anything less than 3.9% means he uses a word less than average. He uses “it’s” and “don’t” a lot less than average. These could be a standardization or a typesetting thing.
In contrast he uses the word “it” 4.2% and “the” 4.1% of the usages – so this is about what you’d expect.
Again, I don’t think this tells us much interesting about Shakespeare. I think it is a useful tool for appreciating the limits of standardization. And I think that this kind of analysis – when applied in a slightly more sophisticated fashion – might turn up interesting things. But that’s the next hack…